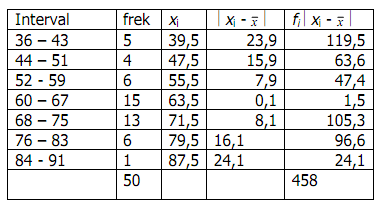
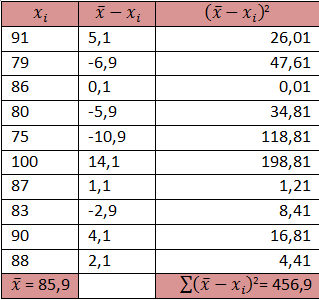
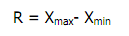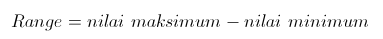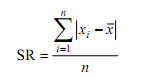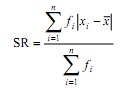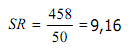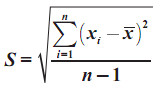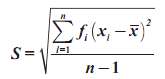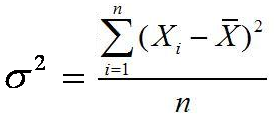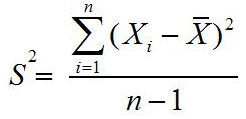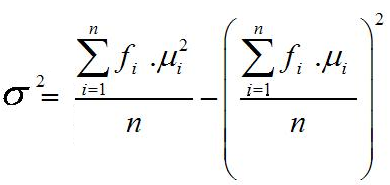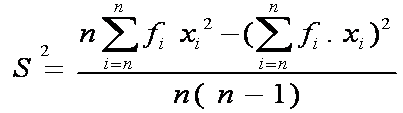TUGAS BAB V MOMEN , KEMIRINGAN DAN KURTORIS

TUGAS BAB V. MOMENT, KEMIRINGAN DAN KURTOSIS

BAB V. MOMENT, KEMIRINGAN DAN KURTOSIS

 Skewness and Kurtosis Rata-rata dan ukuran penyebaran dapat menggambarkan distribusi data tetapi tidak cukup untuk menggambarkan sifat distribusi. Untuk dapat menggambarkan karakteristik dari suatu distribusi data, kita menggunakan konsep-konsep lain yang dikenal sebagai kemiringan (skewness) dan keruncingan (kurtosis). Skewness Kemiringan (skewness) berarti ketidaksimetrisan. Sebuah distribusi dikatakan simetris apabila nilai-nilainya tersebar merata disekitar nilai rata-ratanya. 

Sebagai contoh, distribusi data berikut simetris terhadap nilai rata-ratanya, 3. 

x          1 2 3 4 5

frek f) 5 9 12 9 5 

 Pada contoh gambar berikut, distribusi data tidak simetris. 

Gambar pertama miring (menjulur) ke arah kiri dan gambar ke-2 miring ke arah kanan. Pada distribusi data yang simetris, mean, median dan modus bernilai sama. Beberapa langkah-langkah perhitungan digunakan untuk menyatakan arah dan tingkat kemiringan dari sebaran data. Langkah-langkah tersebut diperkenalkan oleh Pearson. Koefisien kemiringan(Coefficient of Skewness): Interpretasi: Untuk distribusi data yang simetris, Sk = 0. Apabila distribusi data menjulur ke kiri (negatively skewed), Sk bernilai negatif, dan apabila menjulur ke kanan (positively skewed), SK bernilai positif. Kisaran untuk SK antara -3 dan 3. Ukuran kemiringan yang lain adalah koefisien β1 (baca 'beta-satu'): dimana: Interpretasi: Distribusi dikatakan simetris apabila nilai b1 = 0. Skewness positif atau negatif tergantung pada nilai b1 apakah bernilai positif atau negatif. Ukuran Skewness yang sering digunakan: Skewness Populasi: Skewness Sampel: Source: D. N. Joanes and C. A. Gill. "Comparing Measures of Sample Skewness and Kurtosis". The Statistician 47(1):183–189. atau formula berikut (MS Excel): s = standar deviasi NB: kedua formula di atas menghasilkan nilai skewness yang sama Interpretasi: Distribusi dikatakan simetris apabila nilai g1 = 0. Skewness positif atau negatif tergantung pada nilai g1 apakah bernilai positif atau negatif. Menurut Bulmer, M. G., Principles of Statistics (Dover, 1979): 

• highly skewed: jika skewness kurang dari −1 atau lebih dari +1 

• moderately skewed: jika skewness antara −1 dan −½ atau antara +½ dan +1.

 • approximately symmetric: jika skewness is berada di antara −½ dan +½. Kurtosis Kurtosis merupakan ukuran untuk mengukur keruncingan distribusi data. Distribusi pada gambar di atas semuanya simetris terhadap nilai rata-ratanya. Namun bentuk ketiganya tidak sama. Kurva berwarna biru dikenal sebagai mesokurtik (kurva normal), kurva berwarna merah dikenal sebagai leptokurtik (kurva runcing) dan kurva berwarna hijau dikenal sebagai platikurtik (kurva datar). Kurtosis dihitung dengan menggunakan koefisien Pearson, β2 (baca 'beta - dua'). dimana: Ukuran Kurtosis yang sering digunakan: Kurtosis Populasi: Kurtosis: Excess Kurtosis: Kurtosis Sampel: atau formula berikut (MS Excel): s = standar deviasi NB: Excel menggunakan nilai Excess Kurtosis. Hasil perhitungan dari kedua formula di atas, menghasilkan nilai yang sama Interpretasi: Distribusi dikatakan:

 • Mesokurtik (Normal) jika b2 = 3 

• Leptokurtik jika b2 > 3 

• platikurtik jika b2 < 3 Analisis Korelasi Product Moment dalam Statistika Analisis korelasi merupakan salah satu teknik statistik yang digunakan untuk menganalisis hubungan antara dua variabel atau lebih yang bersifat kuantitatif. Salah satu dari analisis korelasi tersebut adalah analisis korelasi product moment (Pearson). Variabel yang digunakan disini terbagi dua yaitu variabel bebas (x) dengan variabel terikat (y), dengan ketentuan data memiliki syarat-syarat tertentu. Korelasi Pearson Product Moment (r) dapat diformulasikan sbb: dengan ketentuan −1 ≤ r ≤ r . Dan interpretasi koefisien korelasi nilai r ini dapat dirangkum dalam tabel berikut: Langkah-langkah yang diperlukan untuk uji korelasi Pearson Product Moment adalah sebagai berikut : 

 1. Rumuskan hipotesis Ha dan Ho dalam bentuk kalimat. 

2. Rumuskan hipotesis Ha dan Ho dalam bentuk statistik. 

3. Buat tabel pembantu. 

4. Tentukan r 

5. Tentukan nilai KP 

6. Lakukan uji signifikansi. 

7. Tentukan α , dengan derajat bebas db = n − 2 . 

 8. Tentukan konklusi

TUGAS BAB VI DISTRIBUSI NORMAL F DAN T

TUGAS BAB VI. DISTRIBUSI NORMAL, DISTRIBUSI T, dan DISTRIBUSI F

BAB VI. DISTRIBUSI NORMAL, DISTRIBUSI T, dan DISTRIBUSI F 

DISTRIBUSI NORMAL

 Distribusi normal adalah distribusi dari variabel acak kontinu. Kadang-kadang distribusi normal disebut juga dengan distribusi Gauss. Distribusi ini merupakan distribusi yang paling penting dan paling banyak digunakan di bidang statistika. Fungsi densitas distribusi normal diperoleh dengan persamaan sebagai berikut: 

dimana π = 3,1416 e = 2,7183 µ = rata-rata σ = simpangan baku Persamaan di atas bila dihitung dan diplot pada grafik akan terlihat seperti pada Gambar 1 berikut: 

Gambar 1. kurva distribusi normal umum 

Sifat-sifat penting distribusi normal adalah sebagai berikut: 

1. Grafiknya selalu berada di atas sumbu x 

2. Bentuknya simetris pada x = µ 

3. Mempunyai satu buah modus, yaitu pada x = µ 

4. Luas grafiknya sama dengan satu unit persegi, dengan rincian 

 a. Kira-kira 68% luasnya berada di antara daerah µ – σ dan µ + σ 

 b. Kira-kira 95% luasnya berada di antara daerah µ – 2σ dan µ + 2σ 

 c. Kira-kira 99% luasnya berada di antara daerah µ – 3σ dan µ + 3σ 

Membuat kurva normal umum bukanlah suatu pekerjaan yang mudah. Lihat saja rumus untuk mencari fungsi densitasnya (nilai pada sumbu Y) begitu rumit. Oleh karena itu, orang tidak banyak menggunakannya. Orang lebih banyak menggunakan DISTIBUSI NORMAL BAKU. Kurva distribusi normal baku diperoleh dari distribusi normal umum dengan cara transformasi nilai x menjadi nilai z, dengan formula sbb: 

 Kurva distribusi normal baku disajikan pada Gambar 2 berikut ini. 

Gambar 2. Kurva distribusi normal baku 

Kurva distribusi normal baku lebih sederhana dibanding kurva normal umum. Pada kurva distribusi normal baku, nilai µ = 0 dan nilai σ=1, sehingga terlihat lebih menyenangkan. Namun, sifat-sifatnya persis sama dengan sifat-sifat distribusi normal umum. Untuk keperluan praktis, para ahli statistika telah menyusun Tabel distribusi normal baku dan tabel tersebut dapat ditemukan hampir di semua buku teks Statistika. Tabel distribusi normal bakui disebut juga dengan Tabel Z dan dapat digunakan untuk mencari peluang di bawah kurva normal secara umum, asal saja nilai µ dan σ diketahui. Sebagai catatan nilai µ dan σ dapat diganti masing-masing dengan nilai dan S. Distribusi t Distribusi t merupakan salah satu pengembangan dari Distribusi z. Secara prinsip penggunaan Distribusi t digunakan untuk membandingkan rata-rata dari dua sampel. Rata-rata dua sampel tersebut dibandingkan untuk mengetahui apakah dua data tersebut mempunyai beda. Distribusi biasanya digunakan untuk data yang banyak sampelnya kurang dari sama dengan 30. t di definisikan sebagai berikut: Dari definisi nilai t di atas, ada beberapa nilai yang perlu kita ketahui: sehingga inputan data di atas sebaiknya anda tahu. 

 Contoh ada nilai siswa sebagai berikut: 

Nilai 66 40 75 64 65 71 66 81 65 50 

Apakah nilai data tersebut rata-ratanya sama dengan data yang lain yang rata-ratanya 60? 

Dari data di atas diperoleh nilai sebagai berikut:

 Misalkan taraf signifikansinya 0.05, nilai derajat kebebasan data tersebut dk = 10 - 1 = 9.

 Dari tabel distribusi t didapatkan : Sedangkan nilai t hitung bisa diperoleh dari : Dari nilai tersebut diperoleh Kesimpulannya data diatas tidak berbeda signifikan dengan data yang rata-rata populasinya 60. Distribusi F (ANOVA) ANOVA kepanjangan dari Analysis of Variance. 

Distribusi yang ditemukan oleh seorang ahli statistika bernama R.A Fisher pada tahun 1920. 

Distribusi F (ANOVA) adalah prosedur statistika untuk menghitung apakah rata-rata hitung drai 3 populasi atau lebih sama atau tidak. Distribusi ini digunakan untuk menguji rata-rata dari tiga atau lebih populasi sekaligus untuk menentukan apakah rata-rata itu sama atau tidak. Distribusi F (ANOVA) terbagi menjadi 2 klasifikasi: 

1. Klasifikasi satu arah Klasifikasi satu arah adalah sebuah klasifikasi pengmatan yang hanya didasarkan pada satu kriteria. 

 2. Klasifikasi dua arah Klasifikasi dua arah adalah suatu pengamatan yang didasarkan pada dua kriteria seperti varietas dan jenis pupuk.suatu pengamatan dapat diklasifikasikan menurut dua criteria dengan menyusun data tersebut menjadi baris dan kolom, kolom menyatakan kriterika klasifikasi yang satu sedangkan baris menyatakan criteria klasifikasi yang lainnya.

TUGAS KULIAH STATISTIKA BAB IV UKURAN PENYIMPANGAN

TUGAS KULIAH STATISTIKA BAB IV UKURAN PENYIMPANGAN

Bab IV : Pengukuran Penyimpangan (Range, Deviasi, Varian)

Posted by vebriana parmita on October 6, 2013

PENGUKURAN PENYIMPANGAN

Pengukuran penyimpangan adalah suatu ukuran yang menunjukkan tinggi  rendahnya perbedaan data yang diperoleh dari rata-ratanya. Ukuran penyimpangan digunakan untuk mengetahui luas penyimpangan data atau homogenitas data. Dua variabel data yang memiliki mean sama belum tentu memiliki kualitas yang sama, tergantung dari besar atau kecil ukuran penyebaran datanya. Ada bebarapa macam ukuran penyebaran data, namun yang umum digunakan adalah standar deviasi.

Macam-macam ukuran penyimpangan data adalah :

1. Jangkauan (range)
2. Simpangan rata-rata (mean deviation)
3. Simpangan baku (standard deviation)
4. Varians (variance)
5. Koefisien variasi (Coefficient of variation)

1. Jangkauan (range)

Range adalah salah satu ukuran statistik yang menunjukan jarak penyebaran data antara nilai terendah (Xmin) dengan nilai tertinggi (Xmax). Ukuran ini sudah digunakan pada pembahasan daftar distribusi frekuensi. Adapun rumusnya adalah

Contoh : 

Berikut ini nilai ujian semester dari 3 mahasiswa
A = 60 55 70 65 50 80 40
B = 50 55 60 65 70 65 55
C = 60 60 60 60 60 60 60

Dari data diatas dapat diketahui bahwa
A = memiliki Xmax=80, Xmin= 40 , R = 40 , meanya 60
B = memiliki Xmax=70, Xmin= 50 , R = 20 , meanya 60
C = memiliki Xmax=60, Xmin= 60 , R = 0 , meanya 60

Dari contoh di atas dapat disimpulkan bahwa :
a. Semakin kecil rangenya maka semakin homogen distribusinya
b. Semakin besar rangenya maka semakin heterogen distribusinya
c. Semakin kecil rangenya, maka meannya merupakan wakil yang representatif
d. Semakin besar rangenya maka meannya semakin kurang representatif

2. Simpangan Rata-rata (mean deviation)

Simpangan rata-rata merupakan penyimpangan nilai-nilai individu dari nilai rata-ratanya. Rata-rata bisa berupa mean atau median. Untuk data mentah simpangan rata-rata dari median cukup kecil sehingga simpangan ini dianggap paling sesuai untuk data mentah. Namun pada umumnya, simpangan rata-rata yang dihitung dari mean yang sering digunakan untuk nilai simpangan rata-rata.

• Data tunggal dengan seluruh skornya berfrekuensi satu

dimana xi merupakan nilai data

• Data tunggal sebagian atau seluluh skornya berfrekuensi lebih dari satu

dimana xi merupakan nilai data

• Data kelompok ( dalam distribusi frekuensi)

dimana xi merupakan tanda kelas dari interval ke-i dan fi merupakan frekuensi interval ke-i

Contoh :

Dari tabel diperoleh 

3. Simpangan Baku (standard deviation)

Standar deviasi merupakan ukuran penyebaran yang paling banyak digunakan. Semua gugus data dipertimbangkan sehingga lebih stabil dibandingkan dengan ukuran lainnya. Namun, apabila dalam gugus data tersebut terdapat nilai ekstrem, standar deviasi menjadi tidak sensitif lagi, sama halnya seperti mean.

Standar Deviasi memiliki beberapa karakteristik khusus lainnya. SD tidak berubah apabila setiap unsur pada gugus datanya di tambahkan atau dikurangkan dengan nilai konstan tertentu. SD berubah apabila setiap unsur pada gugus datanya dikali/dibagi dengan nilai konstan tertentu. Bila dikalikan dengan nilai konstan, standar deviasi yang dihasilkan akan setara dengan hasilkali dari nilai standar deviasi aktual dengan konstan.

Rumus Simpangan Baku untuk Data Tunggal

• untuk data sample menggunakan rumus

• untuk data populasi menggunkan rumus

Contoh :
Selama 10 kali ulangan semester ini sobat mendapat nilai 91, 79, 86, 80, 75, 100, 87, 93, 90,dan 88. Berapa simpangan baku dari nilai ulangan sobat?

Jawab
Soal di atas menanyakan simpangan baku dari data populasi jadi menggunakan rumus simpangan baku untuk populasi.
Kita cari dulu rata-ratanya
rata-rata = (91+79+86+80+75+100+87+93+90+88)/10 = 869/10 = 85,9

Kita masukkan ke rumus

Rumus Simpangan Baku Untuk Data Kelompok

• untuk sample menggunakan rumus

• untuk populasi menggunakan rumus

Contoh :
Diketahui data tinggi badan 50 siswa samapta kelas c adalah sebagai berikut

hitunglah berapa simpangan bakunya

1. Kita cari dulu rata-rata data kelompok tersebut

2. Setelah ketemu rata-rata dari data kelompok tersebut kita bikin tabel untuk memasukkannya ke rumus simpangan baku

4. Varians (variance)

Varians adalah salah satu ukuran dispersi atau ukuran variasi.  Varians dapat menggambarkan bagaimana berpencarnya suatu data kuantitatif.  Varians diberi simbol  σ² (baca: sigma kuadrat) untuk populasi dan untuk s² sampel.

Selanjutnya kita akan menggunakan simbol s²  untuk varians karena umumnya kita hampir selalu berkutat dengan sampel dan jarang sekali berkecimpung dengan populasi.

Rumus varian atau ragam data tunggal untuk populasi

Rumus varian atau ragam data tunggal untuk sampel

Rumus varian atau ragam data kelompok untuk populasi

Rumus varian atau ragam data kelompok untuk sampel

Keterangan:
σ² = varians atau ragam untuk populasi
S² = varians atau ragam untuk sampel
f_i = Frekuensi
x_i = Titik tengah
x¯ = Rata-rata (mean) sampel dan   μ = rata-rata populasi
n =  Jumlah data

5. Koefisien variasi (Coefficient of variation)

Koefisien variasi merupakan suatu ukuran variansi yang dapat digunakan untuk membandingkan suatu distribusi data yang mempunyai satuan yang berbeda. Kalau kita membandingkan berbagai variansi atau dua variabel yang mempunyai satuan yang berbeda maka tidak dapat dilakukan dengan menghitung ukuran penyebaran yang sifatnya absolut.

Koefisien variasi adalah suatu perbandingan antara simpangan baku dengan nilai rata-rata dan dinyatakan dengan persentase.

Besarnya koefisien variasi akan berpengaruh terhadap kualitas sebaran data. Jadi jika koefisien variasi semakin kecil maka datanya semakin homogen dan jika koefisien korelasi semakin besar maka datanya semakin heterogen.

Daftas Pustaka :

Suharyadi, & Purwanto. (2009). In Statistika untuk Ekonomi dan Keuangan Modern. Jakarta: Salemba Empat.

Sudjana. (1991). In Statistika. Bandung: Tarsito.

http://www.smartstat.info/statistika/statisika-deskriptif/ukuran-penyebaran-measures-of-dispersion.html

http://rumushitung.com/2013/04/05/rumus-simpangan-baku/

http://digensia.wordpress.com/2012/03/15/statistik-deskriptif/http://okemath.com/?page_id=394

TUGAS KULIAH STATISTIKA STIESS, VI DISTRIBUSI NORMAL, F DAN T

TUGAS KULIAH STATISTIKA BAB IV UKURAN PENYIMPANGAN

Bab IV : Pengukuran Penyimpangan (Range, Deviasi, Varian)

Posted by vebriana parmita on October 6, 2013

PENGUKURAN PENYIMPANGAN

Pengukuran penyimpangan adalah suatu ukuran yang menunjukkan tinggi  rendahnya perbedaan data yang diperoleh dari rata-ratanya. Ukuran penyimpangan digunakan untuk mengetahui luas penyimpangan data atau homogenitas data. Dua variabel data yang memiliki mean sama belum tentu memiliki kualitas yang sama, tergantung dari besar atau kecil ukuran penyebaran datanya. Ada bebarapa macam ukuran penyebaran data, namun yang umum digunakan adalah standar deviasi.

Macam-macam ukuran penyimpangan data adalah :

1. Jangkauan (range)
2. Simpangan rata-rata (mean deviation)
3. Simpangan baku (standard deviation)
4. Varians (variance)
5. Koefisien variasi (Coefficient of variation)

1. Jangkauan (range)

Range adalah salah satu ukuran statistik yang menunjukan jarak penyebaran data antara nilai terendah (Xmin) dengan nilai tertinggi (Xmax). Ukuran ini sudah digunakan pada pembahasan daftar distribusi frekuensi. Adapun rumusnya adalah

Contoh : 

Berikut ini nilai ujian semester dari 3 mahasiswa
A = 60 55 70 65 50 80 40
B = 50 55 60 65 70 65 55
C = 60 60 60 60 60 60 60

Dari data diatas dapat diketahui bahwa
A = memiliki Xmax=80, Xmin= 40 , R = 40 , meanya 60
B = memiliki Xmax=70, Xmin= 50 , R = 20 , meanya 60
C = memiliki Xmax=60, Xmin= 60 , R = 0 , meanya 60

Dari contoh di atas dapat disimpulkan bahwa :
a. Semakin kecil rangenya maka semakin homogen distribusinya
b. Semakin besar rangenya maka semakin heterogen distribusinya
c. Semakin kecil rangenya, maka meannya merupakan wakil yang representatif
d. Semakin besar rangenya maka meannya semakin kurang representatif

2. Simpangan Rata-rata (mean deviation)

Simpangan rata-rata merupakan penyimpangan nilai-nilai individu dari nilai rata-ratanya. Rata-rata bisa berupa mean atau median. Untuk data mentah simpangan rata-rata dari median cukup kecil sehingga simpangan ini dianggap paling sesuai untuk data mentah. Namun pada umumnya, simpangan rata-rata yang dihitung dari mean yang sering digunakan untuk nilai simpangan rata-rata.

• Data tunggal dengan seluruh skornya berfrekuensi satu

dimana xi merupakan nilai data

• Data tunggal sebagian atau seluluh skornya berfrekuensi lebih dari satu

dimana xi merupakan nilai data

• Data kelompok ( dalam distribusi frekuensi)

dimana xi merupakan tanda kelas dari interval ke-i dan fi merupakan frekuensi interval ke-i

Contoh :

Dari tabel diperoleh 

3. Simpangan Baku (standard deviation)

Standar deviasi merupakan ukuran penyebaran yang paling banyak digunakan. Semua gugus data dipertimbangkan sehingga lebih stabil dibandingkan dengan ukuran lainnya. Namun, apabila dalam gugus data tersebut terdapat nilai ekstrem, standar deviasi menjadi tidak sensitif lagi, sama halnya seperti mean.

Standar Deviasi memiliki beberapa karakteristik khusus lainnya. SD tidak berubah apabila setiap unsur pada gugus datanya di tambahkan atau dikurangkan dengan nilai konstan tertentu. SD berubah apabila setiap unsur pada gugus datanya dikali/dibagi dengan nilai konstan tertentu. Bila dikalikan dengan nilai konstan, standar deviasi yang dihasilkan akan setara dengan hasilkali dari nilai standar deviasi aktual dengan konstan.

Rumus Simpangan Baku untuk Data Tunggal

• untuk data sample menggunakan rumus

• untuk data populasi menggunkan rumus

Contoh :
Selama 10 kali ulangan semester ini sobat mendapat nilai 91, 79, 86, 80, 75, 100, 87, 93, 90,dan 88. Berapa simpangan baku dari nilai ulangan sobat?

Jawab
Soal di atas menanyakan simpangan baku dari data populasi jadi menggunakan rumus simpangan baku untuk populasi.
Kita cari dulu rata-ratanya
rata-rata = (91+79+86+80+75+100+87+93+90+88)/10 = 869/10 = 85,9

Kita masukkan ke rumus

Rumus Simpangan Baku Untuk Data Kelompok

• untuk sample menggunakan rumus

• untuk populasi menggunakan rumus

Contoh :
Diketahui data tinggi badan 50 siswa samapta kelas c adalah sebagai berikut

hitunglah berapa simpangan bakunya

1. Kita cari dulu rata-rata data kelompok tersebut

2. Setelah ketemu rata-rata dari data kelompok tersebut kita bikin tabel untuk memasukkannya ke rumus simpangan baku

4. Varians (variance)

Varians adalah salah satu ukuran dispersi atau ukuran variasi.  Varians dapat menggambarkan bagaimana berpencarnya suatu data kuantitatif.  Varians diberi simbol  σ² (baca: sigma kuadrat) untuk populasi dan untuk s² sampel.

Selanjutnya kita akan menggunakan simbol s²  untuk varians karena umumnya kita hampir selalu berkutat dengan sampel dan jarang sekali berkecimpung dengan populasi.

Rumus varian atau ragam data tunggal untuk populasi

Rumus varian atau ragam data tunggal untuk sampel

Rumus varian atau ragam data kelompok untuk populasi

Rumus varian atau ragam data kelompok untuk sampel

Keterangan:
σ² = varians atau ragam untuk populasi
S² = varians atau ragam untuk sampel
f_i = Frekuensi
x_i = Titik tengah
x¯ = Rata-rata (mean) sampel dan   μ = rata-rata populasi
n =  Jumlah data

5. Koefisien variasi (Coefficient of variation)

Koefisien variasi merupakan suatu ukuran variansi yang dapat digunakan untuk membandingkan suatu distribusi data yang mempunyai satuan yang berbeda. Kalau kita membandingkan berbagai variansi atau dua variabel yang mempunyai satuan yang berbeda maka tidak dapat dilakukan dengan menghitung ukuran penyebaran yang sifatnya absolut.

Koefisien variasi adalah suatu perbandingan antara simpangan baku dengan nilai rata-rata dan dinyatakan dengan persentase.

Besarnya koefisien variasi akan berpengaruh terhadap kualitas sebaran data. Jadi jika koefisien variasi semakin kecil maka datanya semakin homogen dan jika koefisien korelasi semakin besar maka datanya semakin heterogen.

Daftas Pustaka :

Suharyadi, & Purwanto. (2009). In Statistika untuk Ekonomi dan Keuangan Modern. Jakarta: Salemba Empat.

Sudjana. (1991). In Statistika. Bandung: Tarsito.

http://www.smartstat.info/statistika/statisika-deskriptif/ukuran-penyebaran-measures-of-dispersion.html

http://rumushitung.com/2013/04/05/rumus-simpangan-baku/

http://digensia.wordpress.com/2012/03/15/statistik-deskriptif/http://okemath.com/?page_id=394